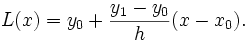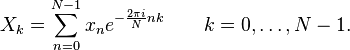METODY NUMERYCZNE I PROBABILISTYCZNE
Metody numeryczne
Metody Numeryczne zajmują się szukaniem i udoskonalaniem sposobów rozwiązywania zadań matematyki za pomocą skończonej liczby działań arytmetycznych i logicznych. Praktyczne wykorzystanie metod numerycznych już od lat wiąże się z maszynami cyfrowymi. Współczesne metody numeryczne są konstruowane z myślą o ich realizacji na maszynach cyfrowych. Wykonanie obliczeń numerycznych na komputerach tworzy nową klasę problemów. Wynikają one między innymi ze stosowanej arytmetyki. Każda liczba w pamięci komputera jest reprezentowana przez swoje skończone rozwinięcie. W każdym działaniu arytmetycznym powstaje błąd, ponieważ wynik jest również skończonym rozwinięciem. Dlatego nie wolno nam przyjmować ich bezkrytycznie, i uważać je za poprawne tylko dlatego, że obliczone zostały przez komputer
Metody probabilistyczne i statystyka
Metody probabilistyczne polegają na zastosowaniu rachunku prawdopodobieństwa do rozwiązywania problemów kombinatorycznych. Na przykład zamiast konstruować explicite jakiś obiekt o żądanych własnościach (kolorowanie grafu, strategię wygrywającą w grze, kod do przesyłania wiadomości itp.) pokazujemy, że losowy wybrany obiekt posiada taką własność z niezerowym prawdopodobieństwem. Tego typu niekonstruktywne techniki, wprowadzone po raz pierwszy przez Paula Erdösa, okazały się niezwykle skuteczne zarówno w czystej matematyce (m. in. w kombinatoryce, grafach losowych, geometrii), jak i w informatyce teoretycznej i algorytmice (np. w teorii złożoności czy algorytmach randomizowanych). Obecnie rachunek prawdopodobieństwa to podstawowe narzędzie z przybornika każdego szanującego się kombinatoryka (i nie tylko).
Metody probabilistyczne i statystyka - test sprawdzający wiedzę
http://cieciura.net/krzyzowki/mp_test2/index.htm
Metody probabilistyczne i statystyka - rozwiązania testów
Test nr 1 - 100%
Test nr 2 - 100%
Test nr 3 - 100%
Test nr 4 - 100%
Test nr 5 - 100%
Test nr 6 - 100%
Test nr 7 - 100%
Test nr 8 - 100%
Test nr 9 - 100%
Test nr 10 - 100%
Przykładowe metody numeryczne:
Interpolacja liniowa szczególny przypadek interpolacji za pomocą funkcji liniowej. Jeśli  określa wartość z przedziału
określa wartość z przedziału  , a
, a  i
i  tablicę wartości danej funkcji, oraz
tablicę wartości danej funkcji, oraz  odstęp pomiędzy argumentami, wówczas liniową interpolację wartości
odstęp pomiędzy argumentami, wówczas liniową interpolację wartości 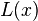 funkcji
funkcji  otrzymujemy jako:
otrzymujemy jako:
 określa wartość z przedziału
określa wartość z przedziału  , a
, a  i
i  tablicę wartości danej funkcji, oraz
tablicę wartości danej funkcji, oraz  odstęp pomiędzy argumentami, wówczas liniową interpolację wartości
odstęp pomiędzy argumentami, wówczas liniową interpolację wartości  funkcji
funkcji  otrzymujemy jako:
otrzymujemy jako: Metoda Monte Carlo (MC) jest stosowana do modelowania
matematycznego procesów zbyt złożonych (obliczania całek, łańcuchów
procesów statystycznych), aby można było przewidzieć ich wyniki za
pomocą podejścia analitycznego. Istotną rolę w metodzie MC odgrywa
losowanie (wybór przypadkowy) wielkości charakteryzujących proces, przy
czym losowanie dokonywane jest zgodnie z rozkładem, który musi być
znany.
Metoda Monte Carlo (MC) jest stosowana do modelowania
matematycznego procesów zbyt złożonych (obliczania całek, łańcuchów
procesów statystycznych), aby można było przewidzieć ich wyniki za
pomocą podejścia analitycznego. Istotną rolę w metodzie MC odgrywa
losowanie (wybór przypadkowy) wielkości charakteryzujących proces, przy
czym losowanie dokonywane jest zgodnie z rozkładem, który musi być
znany.
Typowym przykładem może być modelowanie wyniku zderzenia cząstki o
wysokiej energii z jądrem złożonym, gdzie każdy akt zderzenia
elementarnego (z pojedynczym nukleonem
jądra) modelowany jest oddzielnie poprzez losowanie liczby, rodzaju,
kąta emisji, energii itp. cząstek wtórnych emitowanych w wyniku takiego
zderzenia. Następnym etapem jest modelowanie losu każdej z
cząstek wtórnych (w wyniku kolejnego losowania prawdopodobieństwa
oddziaływania lub wyjścia z jądra). Kontynuując taką procedurę można
otrzymać pełny opis "sztucznie generowanego" procesu złożonego. Po
zebraniu dostatecznie dużej liczby takich informacji można zestawić ich
charakterystyki z obserwowanymi wynikami doświadczalnymi, potwierdzając
lub negując słuszność poczynionych w całej procedurze założeń.
Metoda została opracowana i pierwszy raz zastosowana przez Stanisława Ulama.
 Interpolacja wielomianowa, nazywana też interpolacją Lagrange'a, od nazwiska pioniera badań nad interpolacją Josepha Lagrange'a, lub po prostu interpolacją jest metodą numeryczną przybliżania funkcji tzw. wielomianem Lagrange'a stopnia n, przyjmującym w n+1 punktach, zwanych węzłami interpolacji wartości takie same jak przybliżana funkcja.
Interpolacja wielomianowa, nazywana też interpolacją Lagrange'a, od nazwiska pioniera badań nad interpolacją Josepha Lagrange'a, lub po prostu interpolacją jest metodą numeryczną przybliżania funkcji tzw. wielomianem Lagrange'a stopnia n, przyjmującym w n+1 punktach, zwanych węzłami interpolacji wartości takie same jak przybliżana funkcja.
Interpolacja jest często stosowana w naukach doświadczalnych, gdzie
dysponuje się zazwyczaj skończoną liczbą danych do określenia zależności
między wielkościami.
Zgodnie z twierdzeniem Weierstrassa dowolną funkcję y=f(x) ciągłą na przedziale domkniętym można dowolnie przybliżyć za pomocą wielomianu odpowiednio wysokiego stopnia.
Szybka transformacja Fouriera (ang. FFT od Fast Fourier Transform) to algorytm liczenia dyskretnej transformaty Fouriera oraz transformaty do niej odwrotnej.
Czasem używana jest też forma szybka transformata Fouriera w odniesieniu do tej metody. Ściśle jednak transformacja jest przekształceniem, a transformata wynikiem tego przekształcenia.
Niech x0, ...., xN-1 będą liczbami zespolonymi, wtedy dyskretna transformata Fouriera jest określona wzorem
Obliczanie tych sum za pomocą powyższego wzoru zajęłoby O(N2) operacji.
Algorytmy (jak algorytm Cooleya-Tukeya) obliczające szybką transformację Fouriera bazują na metodzie dziel i zwyciężaj rekurencyjnie dzieląc transformatę wielkości N = N1N2 na transformaty wielkości N1 i N2 z wykorzystaniem O(N) operacji mnożenia.
Całkowanie metodą Simpsona – jedna z metod przybliżania wartości całki oznaczonej funkcji rzeczywistej.
Metoda ma zastosowanie do funkcji stablicowanych w nieparzystej
liczbie równo odległych punktów (wliczając końce przedziału całkowania).
Metoda opiera się na przybliżaniu funkcji całkowanej przez interpolację wielomianem drugiego stopnia.
Znając wartości  funkcji
funkcji  w 3 punktach
w 3 punktach  (przy czym
(przy czym  ), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale
), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale ![[x_0,x_2]](http://upload.wikimedia.org/math/d/e/4/de4217d1fd45f2a6f7c8fa30de546aca.png) , otrzymuje przybliżoną wartość całki:
, otrzymuje przybliżoną wartość całki:
 funkcji
funkcji  w 3 punktach
w 3 punktach  (przy czym
(przy czym  ), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale
), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale ![[x_0,x_2]](http://upload.wikimedia.org/math/d/e/4/de4217d1fd45f2a6f7c8fa30de546aca.png) , otrzymuje przybliżoną wartość całki:
, otrzymuje przybliżoną wartość całki:
Błąd, który przy tym popełniamy, jest równy:  , gdzie:
, gdzie:
 , gdzie:
, gdzie:![c \in [x_0; x_2]](http://upload.wikimedia.org/math/4/5/8/45806695961ce8839e4585b999e8d6d4.png) .
.
Nie znamy położenia punktu c, więc posługujemy się poniższym szacowaniem, mającym zastosowanie w obliczeniach numerycznych:
![R \leqslant \frac{1}{90} h^5 \max_{x \in [x_0; x_2]} |f^{(4)}(x)|](http://upload.wikimedia.org/math/d/9/8/d98b6f6645b6f1caea5c0b00d42a7e05.png) .
.- Kwadraturami Gaussa nazywamy metody całkowania numerycznego polegające na takim wyborze wag
 i węzłów interpolacji
i węzłów interpolacji ![t_1, t_2, \ldots, t_n \in [a,b]](http://upload.wikimedia.org/math/a/e/1/ae1c9f6951bd62c10e063db2033c6973.png) aby wyrażenie
aby wyrażenie 
najlepiej przybliżało całkę
gdzie  jest dowolną funkcją określoną na odcinku
jest dowolną funkcją określoną na odcinku ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , a
, a  jest tzw. funkcją wagową spełniającą warunki
jest tzw. funkcją wagową spełniającą warunki
 jest dowolną funkcją określoną na odcinku
jest dowolną funkcją określoną na odcinku ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , a
, a  jest tzw. funkcją wagową spełniającą warunki
jest tzw. funkcją wagową spełniającą warunki ,
, jest skończona,
jest skończona,- Jeżeli
 jest wielomianem takim, że
jest wielomianem takim, że ![\forall_{x\in [a,b]}\;p(x)\ge 0](http://upload.wikimedia.org/math/7/d/2/7d24afd04dc7bc7d989ae05ec964b18b.png) , to jeśli
, to jeśli  , mamy wtedy
, mamy wtedy  .
.