Metody numeryczne i probabilistyczne: 2013

Wektory i własności własne

Wektory i wartości własne – wielkości opisujące endomorfizm danej przestrzeni liniowej; wektor własny przekształcenia można rozumieć jako wektor, którego kierunek nie ulega zmianie po przyłożeniu do niego endomorfizmu; wartość własna odpowiadająca temu wektorowi to skala podobieństwa tych wektorów. Najczęściej przekształcenie liniowe wyraża się jako macierz, która działa na wektory; wówczas stosuje się nazwy wektor własny macierzy, wartość własna macierzy. W innych teoriach przekształcenia i elementy przestrzeni liniowej mogą mieć inne nazwy. Mówi się wtedy przykładowo o stanach własnych operatora, funkcjach własnych funkcjonału itp.
Definicje
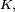Niech $\scriptstyle X$ będzie przestrzenią liniową nad ciałem $\scriptstyle K,$ zaś $\scriptstyle \mathrm T$ oznacza pewien jej endomorfizm, tzn. przekształcenie liniowe tej przestrzeni w siebie. Jeśli dla pewnego niezerowego wektora $\scriptstyle x$ przestrzeni spełniony jest warunek

$\mathrm Tx = \lambda x,$

gdzie $\scriptstyle \lambda$ jest pewnym skalarem, to $\scriptstyle x$ nazywa się wektorem własnym, a $\scriptstyle \lambda$ nazywa się wartością własną przekształcenia $\scriptstyle \mathrm T.$
Danej wartości własnej $\scriptstyle \lambda$ operatora $\scriptstyle \mathrm T$ odpowiada zbiór

$X_\lambda(T) = \{x\in X\colon Tx = \lambda x\}$

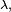nazywany podprzestrzenią własną odpowiadającą wartości własnej $\scriptstyle \lambda,$ gdyż tworzy on domkniętą podprzestrzenią liniową przestrzeni $\scriptstyle X.$ Jej wymiar nazywa się wielokrotnością wartości własnej $\lambda.$
Często zakłada się, że 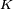$\scriptstyle K$ jest ciałem liczb rzeczywistych bądź zespolona, zaś na $\scriptstyle X$ określona jest topologia liniowa. W zastosowaniach (np. równania różniczkowe) bada się często wartości własne operatorów liniowych określonych na przestrzeniach Banacha, Hilberta itp. W dalszej części artykułu będziemy zakładać ogólnie, że $\scriptstyle X$ jest pewną przestrzenią Banacha, a $\scriptstyle \mathrm T\colon X\to X$ jest ustalonym operatorem liniowym i ciągłym.

Własności

Jeżeli $\scriptstyle \mathrm T$ jest samosprzężonym operatorem liniowym na przestrzeni Hilberta $\scriptstyle X,$ to wartości własne tego operatora są rzeczywiste, ponadto wektory własne, odpowiadające różnym wartościom własnym są ortogonalne.
Jeżeli $\scriptstyle \lambda \in K$ jest wartością własną operatora $\scriptstyle \mathrm T,$ to $\scriptstyle |\lambda|\leqslant \|\mathrm T\|$ (założenie zupełności przestrzeni jest tu nieistotne).
Liczba $\scriptstyle \lambda \in K$ jest wartością własną operatora $\scriptstyle \mathrm T$ wtedy i tylko wtedy, gdy operator $\scriptstyle \mathrm T_\lambda = \lambda I-T$ nie jest różnowartościowy.
Wektory własne odpowiadające różnym wartościom własnym są liniowo niezależne.
Jeśli macierz $\scriptstyle \mathbf A$ potraktować jako macierz przekształcenia liniowego pewnej przestrzeni liniowej $\scriptstyle V,$ to wektory własne odpowiadające tej samej wartości własnej tworzą podprzestrzeń.
Jeśli suma wymiarów podprzestrzeni z powyższej własności jest równa wymiarowi $\scriptstyle V,$ to wektory własne odpowiadające różnym wartościom własnym tworzą bazę tej przestrzeni

Rachunek prawdopodobieństwa

Rachunek prawdopodobieństwa to dział matematyki zajmujący się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe. A doświadczenie jest losowe, jeżeli można je wielokrotnie powtarzać w tych samych warunkach i wyniku doświadczenia nie potrafimy z góry przewidzieć. Przykładem takich doświadczeń jest rzut monetą, rzut kostką do gry, losowanie karty z talii kart, itp.

Pierwsze znane zagadnienia z rachunku prawdopodobieństwa dotyczyły gier hazardowych, w szczególności gry w kości. Mimo, że gra znana była już w starożytności, pierwsze teoretyczne zainteresowanie tą grą przejawiali dopiero matematycy francuscy z XVII w. Pierre de Fermat i Blaise Pascal. Podstawowymi pojęciami rachunku prawdopodobieństawa są: przestrzeń zdarzeń elementarnych, z jej elementami, doświadczenie oraz zdarzenie losowe, prawdopodobieństwo zajścia określonego zdarzenia.

Prawdopodobieństwo warunkowe

W wielu przypadkach, informacja o zajściu zdarzenia B ma pewien wpływ na wartość obliczonego prawdopodobieństwa zdarzenia A. Zdarzenie polegające na zajściu zdarzenia A przy założeniu, że zaszło zdarzenie B, oznaczamy symbolem A|B, prawdopodobieństwo tego zdarzenia P(A|B) nazywamy prawdopodobieństwem warunkowym
Prawdopodobieństwem zajścia zdarzenia A pod warunkiem, że zdarzenie B zajdzie, nazywamy liczbę

P (A | B) = \frac{P (A \cap B)}{P (B)}

gdzie A, B ⊂ Ω, P(B) > 0.
Z definicje tej wynika, że P(A|B) ≥ 0, P(B|B) = 1, oraz dla każdej pary wykluczających się zdarzeń A, C ⊂ B
P(A ∪ C|B) = P(A|B) + P(C|B)
Zatem funkcja przyporządkowująca każdemu zdarzeniu A ⊂ B liczbę P(A|B) jest prawdopodobieństwem określonym na zdarzeniach w zbiorze B.
W modelu klasycznym, tzn. gdy wszystkie możliwe wyniki są jednakowo prawdopodobne, prawdopodobieństwo warunkowe można obliczyć ze wzoru:

P (A | B) = \frac{\overset{=}{A \cap B}}{\overset{=}{B}}

.

Ze wzoru na prawdopodobieństwo warunkowe otrzymujemy wzór na prawdopodobieństwo iloczynu zdarzeń:
Jeżeli A, B ⊂ Ω, P(B) > 0, to P(A ∩ B) = P(A|B) · P(B)

Podstawy teorii weryfikacji hipotez statystycznych

Hipotezą statystyczną nazywamy każdą taką hipotezę, która dotyczy bądź postaci rozkładu, bądź wartości parametrów rozkładu pewnej zmiennej losowej i która może być weryfikowana statystycznie, to znaczy w oparciu o wyniki zaobserwowane w próbie.
Testem statystycznym nazywamy każdą jednoznacznie zdefiniowaną regułę postępowania określającą warunki przy których należy weryfikowaną hipotezę przyjąć bądź odrzucić. Weryfikacja hipotez statystycznych odbywa się na podstawie wyników zaobserwowanych w próbie. W rezultacie test statystyczny podaje reguły, przy jakiego rodzaju wynikach próby sprawdzaną hipotezę się przyjmuje, a przy jakich odrzuca.
Weryfikowaną hipotezę nazywa się zwykle hipotezą zerową: H0
D e cy z j a
Hipoteza H0 Przyjąć H0 Odrzucić H0
Jest prawdziwa Decyzja poprawna Błąd I rodzaju. Prawdopodobieństwo popełnienia tego błędu =

Jest fałszywa Błąd II rodzaju Decyzja poprawna

Wartość prawdopodobieństwa popełnienia błędu I rodzaju - nazywamy poziomem istotności testu; najczęściej przyjmuje się = 0,05 , lub = 0,1.
Oprócz hipotezy zerowej formułujemy również hipotezę H1 ( hipotezę alternatywna), którą skłonni jesteśmy przyjąć, jeśli weryfikowaną hipotezę H0 należy odrzucić.
Sprawdzian hipotezy jest to pewna funkcja wyników z próby, na podstawie której decydujemy, czy można hipotezę H0 przyjąć, czy odrzucić. Przez obszar krytyczny rozumie się taki zbiór wartości sprawdzianu hipotezy, że jeżeli zaobserwowana wartość sprawdzianu znajdzie się w tym obszarze, to odrzuca się hipotezę H0 na korzyść H1. Prawdopodobieństwo tego, że sprawdzian przyjmie wartość należącą do obszaru krytycznego, jest przy założeniu prawdziwości hipotezy H0 równe założonemu poziomowi istotności

Przykład

Należy dokonać oceny partii pudelek zapalek liczącej 100 tys. sztuk. dostawca twierdzi, że w pudelku znajdują się przecietnie 54 zapalki. Zweryfikować hipotezę

H 0 (m = m 0 = 54)

. Ponieważ nie znamy rozkładu liczby zapałek w pudełkach w populacji generalnej, a mozemy łatwo pobrać próbę >= 30 możemy wieć w przybliżeniu skorzystać z rozkładu normalnego. Zkaldamy, że przy próbie o wielkości n = 100 odnotowano średnią arytmetyczną

m n = 51,21

natomiast

σ n' = 2,54

. Weryfikujemy przy poziomie istotności

α = 0,02

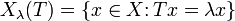
ponieważ obraliśmy dużą próbę wiec $\sigma_{M_n} \approx {{\sigma_n'} \over { \sqrt{n}}} = 0{,}245$ . Musimy zatem wyznaczyć t dla ktorego $P \left ( {{|M_n-m_0|} \over {\sigma_{M_n}}} \ge t \right ) = 0{,}02$
Definiujemy unormowaną zmienną Y:
$Y={{M_n-m_0} \over {\sigma_{M_n}}}$
podstawiamy do wzoru
$P(|Y| \ge t) = 0{,}02$
Z własności bezwzględnej wartości:
$P[(Y \ge t) \vee (Y \le -t)] = 0{,}02$
$P(Y \ge t)+P(Y \le -t) = 0{,}02$
Ponieważ funkcja gęstości jest dla rozkładu N(0,1) parzysta to zachodzi równość:
$P(Y \ge t) = P(Y \le -t)$
$2P(Y \ge t) = 0{,}02$
$P(Y \ge t) = 0{,}01$
Wiadomo, że P(A) to to samo co 1-P(A') więc:

1 - P (Y < t) = 0,01

P (Y < t) = 0,99

A P(Y<x) to dystrybuanta - czyli F(x):

F (t) = 0,99

Teraz w tablicy rozkładu normalnego znajdujemy najmniejszą wartość t dla której F(t) wynosi conajmniej 0,99. Jest to wartość 2,33.
Hipotezę

H 0

należy wiec odrzucić na poziomie istotności

α

jeżeli $|M_n - 54| \ge t \cdot 0{,}245$ , w przeciwnym wypadku przy zadanej istotności

α = 0,02

nie możemy ani potwierdzić hipotezy, ani jej odrzucić.
Zgodnie z naszymi danymi wychodzi:

| M n - 54 | = | 51,21 - 54 | = 2,79

$\sigma_{M_n} \cdot t = 0{,}245 \cdot 2{,}33 = 0{,}57085$
Więc:
$| M_n - 54 | \ge \sigma_{M_n} \cdot t$
$2{,}79 \ge 0{,}57085$
Zatem hipotezę możemy odrzucić (jeśli wyjdzie odwrotnie to piszemy że nie odrzucamy ani nie potwierdzamy - tak właśnie trzeba było zrobić na egzaminie, bo wychodziło <).

niedziela, 13 stycznia 2013

Wektory i własności własne

Rachunek prawdopodobieństwa

Prawdopodobieństwo warunkowe

Podstawy teorii weryfikacji hipotez statystycznych

Przykład