Metody numeryczne i probabilistyczne: Układy równań liniowych

Układy równań liniowych

Czasem zadania obliczeniowe wymagają wykonania naprawdę wielkiej liczby obliczeń zmiennoprzecinkowych, przy czym wiele znanych, matematycznie równoważnych metod rozwiązywania takich zadań, ma diametralnie różne własności numeryczne. Bardzo ważną klasą takich intensywnych obliczeniowo zadań jest rozwiązywanie układów równań liniowych

$\displaystyle Ax = b,$

gdzie $\displaystyle A$ jest nieosobliwą macierzą $\displaystyle N\times N$ , a dany wektor prawej strony $\displaystyle b\in R^N$ .
W praktyce spotyka się zadania z $\displaystyle N = 2, 3, \ldots 1000$ . Zdarzają się także czasem szczególne macierze o wymiarach nawet rzędu $\displaystyle 10^8$ ! Rozwiązywanie układów równań liniowych jest sercem wielu innych algorytmów numerycznych --- podobno szacuje się, że około 75 procent czasu obliczeniowego superkomputerów jest wykorzystywanych właśnie na rozwiązywanie takich zadań. O tym, jak skutecznie rozwiązywać takie zadania, jakie mogą czekać nas niespodzianki, traktują: ten i następne trzy wykłady.
Okazuje się, że kilka znanych w matematyce sposobów rozwiązywania układów równań liniowych, takich jak:

metoda wyznacznikowa (wzory Cramera)
obliczenie macierzy $\displaystyle A^{-1}$ i następnie $\displaystyle x = A^{-1}b$

nie nadaje się do numerycznego rozwiązywania takich zadań. Wkrótce dowiesz się, że jedną z dobrych metod jest metoda eliminacji Gaussa.

Proste układy równań

Niektóre układy równań można bardzo łatwo rozwiązać. Zgodnie z zasadą, że

trudne zadania rozwiązujemy sprowadzając je do sekwencji łatwych zadań,

w dalszej kolejności pokażemy, jak dowolny układ równań sprowadzić do sekwencji dwóch (czasem trzech) łatwych do rozwiązania układów równań. Ale... jakie układy równań są "łatwe"?

Układy z macierzą trójkątną

Rozważmy układ z macierzą trójkątną $\displaystyle A$ . Będą nas szczególnie interesować macierze trójkątne górne, dla których $\displaystyle a_{i,j}=0$ gdy $\displaystyle i>j$ , oraz macierze trójkątne dolne z jedynkami na przekątnej, tzn. $\displaystyle a_{i,j}=0$ , $\displaystyle i<j$ , oraz $\displaystyle a_{i,i}=1$ . Macierze pierwszego rodzaju będziemy oznaczać przez $\displaystyle U$ , a drugiego rodzaju przez $\displaystyle L$ .

$\displaystyle L = \begin{pmatrix} 1 & & & & & \\ * & 1 & & & & \\ * & * & 1 & & & \\ * & * & * & 1 & & \\ \vdots & \vdots & \vdots & \ddots & \ddots & \\ * & * & * & \cdots & * & 1 \end{pmatrix} , \qquad U = \begin{pmatrix} * & * & * & * & \cdots & * \\ & * & * & * & \cdots & * \\ & & * & * & \cdots & * \\ & & & * & \ddots & \vdots \\ & & & & \ddots & * \\ & & & & & * \end{pmatrix}$

Układ z nieosobliwą macierzą trójkątną górną

$\displaystyle U\, x\;=\; c,$

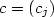
$\displaystyle U=(u_{i,j})$ , $\displaystyle c=(c_j)$

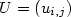Układy z macierzą ortogonalną

Równie tanio można rozwiązać układ równań

$\displaystyle Q x = b,$

gdy $\displaystyle Q$ jest macierzą ortogonalną, to znaczy $\displaystyle Q^TQ = I$ . Rzeczywiście, z ortogonalności wynika wprost, że

$\displaystyle x = Q^T b$

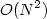i w konsekwencji $\displaystyle x$ można wyznaczyć kosztem takim, jak koszt mnożenia macierzy przez wektor, czyli $\displaystyle O(N^2)$ operacji.
Podobnie, gdy $\displaystyle Q\in C^{N\times N}$ jest unitarna, to znaczy $\displaystyle Q^*Q = I$ (przypomnijmy: $\displaystyle Q^*$ oznacza macierz sprzężoną do $\displaystyle Q$ , tzn. taką, że $\displaystyle Q^*_{ij} = \bar{Q}_{ji}$ ), rozwiązaniem układu równań jest

$\displaystyle x = Q^* b.$

Metoda eliminacji Gaussa

W ogólnym przypadku, bardzo dobrym algorytmem numerycznego rozwiązywania układu równań

$\displaystyle Ax=b$

okazuje się popularna eliminacja Gaussa. Jednak z powodów, które okażą się dla nas później jasne, algorytm ten wyrazimy w terminach tzw. rozkładu LU macierzy, to znaczy sprowadzającego zadanie do znalezienia macierzy trójkątnej dolnej $\displaystyle L$ (z jedynkami na diagonali) oraz trójkątnej górnej $\displaystyle U$ takich, że

$\displaystyle A = LU,$

a następnie rozwiązania sekwencji dwóch układów równań z macierzami trójkątnymi:
Przypuśćmy, że taki rozkład $\displaystyle A=LU$ istnieje (nie musi!). Wówczas, zapisując macierze w postaci blokowej, eksponując pierwszy wiersz i pierwszą kolumnę zaangażowanych macierzy, mamy

$\displaystyle \begin{pmatrix} a_{11} & a_{12}^T\\ a_{21} & A_{22} \end{pmatrix} = \begin{pmatrix} 1 & 0^T\\ l_{21} & L_{22} \end{pmatrix} \begin{pmatrix} u_{11} & u_{12}^T\\ 0 & U_{22}, \end{pmatrix}$

skąd (mnożąc blokowo macierz $\displaystyle L$ przez $\displaystyle U$ ) wynika, że

$\displaystyle u_{11} = a_{11}$ oraz $\displaystyle u_{12} = a_{12}$ , więc pierwszy wiersz $\displaystyle U$ jest kopią pierwszego wiersza $\displaystyle A$ ,
$\displaystyle l_{21} = a_{21}/u_{11}$ , więc pierwsza kolumna $\displaystyle L$ powstaje przez podzielenie wszystkich elementów wektora $\displaystyle a_{21}$ przez element na diagonali $\displaystyle a_{11}$ ,
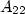$\displaystyle A_{22} - l_{21}u_{12}^T = L_{22}U_{22}$ , a więc znalezienie podmacierzy $\displaystyle L_{22}$ oraz $\displaystyle U_{22}$ sprowadza się do znalezienia rozkładu LU zmodyfikowanego bloku $\displaystyle A_{22}$ macierzy $\displaystyle A$ , wymiaru $\displaystyle (N-1)\times (N-1)$ . Macierz $\displaystyle A_{22} - l_{21}u_{12}^T$ nazywamy uzupełnieniem Schura.

Dostajemy więc algorytm rekurencyjny, jednak ze względu na to, że wywołanie rekurencyjne następuje na końcu, można je zastąpić pętlą. Jest to ważne w praktyce numerycznej, gdyż rekurencja kosztuje: zarówno pamięć, jak i czas.
Ponadto zauważmy, że opisany algorytm możemy wykonać in situ (w miejscu), nadpisując elementy $\displaystyle A$ elementami macierzy $\displaystyle U$ i $\displaystyle L$ (jedynek z diagonali $\displaystyle L$ nie musimy pamiętać, bo wiemy a priori, że tam są). Dzięki temu dodatkowo zaoszczędzimy pamięć.
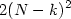Łatwo przekonać się, że $\displaystyle k$ -ty obrót zewnętrznej pętli (tzn. $\displaystyle k$ -ty krok algorytmu rozkładu LU) kosztuje rzędu $\displaystyle 2(N-k)^2$ operacji arytmetycznych, skąd łączny koszt tego algorytmu rozkładu LU wynosi około $\displaystyle \frac{4}{3}N^3$ .
Jeśli więc do rozwiązywania układu równań $\displaystyle Ax=b$ wykorzystamy rozkład LU, to mamy następujące zestawienie kosztów:

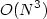Koszt znalezienia rozkładu $\displaystyle A=LU$ : $\displaystyle O(N^3)$ ;
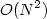Koszt rozwiązania układu $\displaystyle Ly=b$ : $\displaystyle O(N^2)$ ;
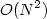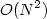Koszt rozwiązania układu $\displaystyle Ux=y$ : $\displaystyle O(N^2)$ .

Tak więc, gdy znany już jest rozkład LU macierzy, koszt rozwiązania równania wynosi już tylko $\displaystyle O(N^2)$ .

Wybór elementu głównego

Opisany powyżej algorytm rozkładu LU czasem może się niestety załamać: mianowicie wtedy, gdy napotka w czasie działania zerowy element w lewym górnym rogu zmodyfikowanej podmacierzy. Na przykład, macierz

$\displaystyle A = \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}$

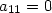jest ewidentnie nieosobliwa, ale nasz algorytm nawet nie ruszy z miejsca, bo od razu zetknie się z dzieleniem przez $\displaystyle a_{11}=0$ ... Ale wystarczy zamienić ze sobą wiersze macierzy $\displaystyle A$ (to znaczy, w układzie równań, zamienić kolejność równań), a dostaniemy macierz, z którą nasz algorytm poradzi sobie bez problemu! Musimy więc --- aby stosować eliminację Gaussa do dowolnych macierzy nieosobliwych --- dokonywać takich permutacji równań, by elementem, przez który dzielimy, była zawsze liczba niezerowa (jest to możliwe, na mocy założenia nieosobliwości macierzy).
W praktyce obliczeniowej, aby uzyskać algorytm o możliwie dobrych własnościach numerycznych, wykorzystujemy tzw. strategię wyboru elementu głównego w kolumnie. Polega to na tym, że zanim wykonamy $\displaystyle k$ -ty krok algorytmu rozkładu LU,

w pierwszej kolumnie podmacierzy $\displaystyle A(k:N,k:N)$ szukamy elementu o największym module (taki element, na mocy założenia nieosobliwości macierzy, jest niezerowy) --- to jest właśnie element główny
zamieniamy ze sobą wiersz 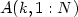$\displaystyle A(k,1:N)$ z wierszem, w którym znajduje się element główny
zapamiętujemy dokonaną permutację, bo potem --- gdy już przyjdzie do rozwiązywania układu równań --- będziemy musieli dokonać analogicznej permutacji wektora prawej strony

Wynikiem takiego algorytmu jest więc rozkład

$\displaystyle PA = LU,$

gdzie $\displaystyle P$ jest pewną (zerojedynkową) macierzą permutacji (tzn. macierzą identyczności z przepermutowanymi wierszami).
Oprócz wyboru elementu głównego w kolumnie, stosuje się czasem inne strategie, m.in. wybór w wierszu (analogicznie) oraz tzw. wybór pełny, gdy elementu głównego szukamy w całej podmacierzy $\displaystyle A(k:N,k:N)$ , co znacznie zwiększa liczbę porównań niezbędnych do wskazania elementu głównego, ale też trochę poprawia własności numeryczne takiego algorytmu.
W praktyce, do przechowywania całej informacji o wykonanych permutacjach wystarcza pojedynczy wektor.

Złożoność obliczeniowa zadania rozwiązania układu równań liniowych

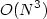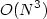Z powyższego wynika, że łączny koszt rozwiązania równania liniowego poprzez rozkład LU wynosi $\displaystyle O(N^3)$ . Można zastanawiać się, jaka jest najmniejsza możliwa liczba operacji zmiennoprzecinkowych potrzebnych do rozwiązania układu równań liniowych.

Można pokazać, że minimalny koszt rozwiązania układu $\displaystyle N$ równań liniowych nie może być wyższego rzędu niż minimalny koszt mnożenia dwóch macierzy $\displaystyle N\times N$ . Tymczasem znany jest całkiem prosty algorytm rekurencyjny, wyznaczający iloczyn dwóch macierzy kosztem $\displaystyle 4.7\cdot N^{log_27} \approx 4.7 \cdot N^{2.807}$ (algorytm Strassena). Bardziej skomplikowany (i praktycznie nieimplementowalny) algorytm Coppersmitha i Winograda daje nawet koszt $\displaystyle O(N^{2.376})$ . Równania liniowe daje się więc (teoretycznie) rozwiązać kosztem $\displaystyle O(N^{2.376})$ .

Jednak w praktyce nawet prosty algorytm Strassena zazwyczaj nie jest stosowany. Wynika to stąd, że ma trochę gorsze własności numeryczne oraz, co istotniejsze, wymaga dużo dodatkowej pamięci na przechowywanie pośrednich wyników. Są jednak podejmowane wysiłki, by zmniejszyć te ograniczenia algorytmu Strassena.

Metody numeryczne i probabilistyczne

poniedziałek, 3 grudnia 2012

Układy równań liniowych