poniedziałek, 26 listopada 2012
poniedziałek, 19 listopada 2012
Aproksymacja
Aproksymacja – proces określania rozwiązań przybliżonych na podstawie rozwiązań znanych, które są bliskie rozwiązaniom dokładnym w ściśle sprecyzowanym sensie. Zazwyczaj aproksymuje się byty (np. funkcje) skomplikowane bytami prostszymi.
Zadanie najlepszej aproksymacji
Niech dana będzie przestrzeń liniowa  z normą
z normą  i niech
i niech  będzie podprzestrzenią liniową
będzie podprzestrzenią liniową  skończonego wymiaru. Zadanie najlepszej aproksymacji polega na znalezieniu takiego
skończonego wymiaru. Zadanie najlepszej aproksymacji polega na znalezieniu takiego  (elementu najlepszej aproksymacji dla danego
(elementu najlepszej aproksymacji dla danego  ), że zachodzi:
), że zachodzi:
 z normą
z normą  i niech
i niech  będzie podprzestrzenią liniową
będzie podprzestrzenią liniową  skończonego wymiaru. Zadanie najlepszej aproksymacji polega na znalezieniu takiego
skończonego wymiaru. Zadanie najlepszej aproksymacji polega na znalezieniu takiego  (elementu najlepszej aproksymacji dla danego
(elementu najlepszej aproksymacji dla danego  ), że zachodzi:
), że zachodzi:
Należy przez to rozumieć, że element  jest elementem "najbliższym" do aproksymowanego
jest elementem "najbliższym" do aproksymowanego  spośród wszystkich elementów
spośród wszystkich elementów  .
.
 jest elementem "najbliższym" do aproksymowanego
jest elementem "najbliższym" do aproksymowanego  spośród wszystkich elementów
spośród wszystkich elementów  .
.
Zadanie najlepszej aproksymacji jest zawsze rozwiązywalne tzn. dla każdego  istnieje element najlepszej aproksymacji
istnieje element najlepszej aproksymacji  ,
ale niekoniecznie jest on jedyny. Należy zauważyć, że element
najlepszej aproksymacji zależy od normy, jaka została przyjęta w
przestrzeni
,
ale niekoniecznie jest on jedyny. Należy zauważyć, że element
najlepszej aproksymacji zależy od normy, jaka została przyjęta w
przestrzeni  .
.
 istnieje element najlepszej aproksymacji
istnieje element najlepszej aproksymacji  ,
ale niekoniecznie jest on jedyny. Należy zauważyć, że element
najlepszej aproksymacji zależy od normy, jaka została przyjęta w
przestrzeni
,
ale niekoniecznie jest on jedyny. Należy zauważyć, że element
najlepszej aproksymacji zależy od normy, jaka została przyjęta w
przestrzeni  .
.Zadanie najlepszej aproksymacji w przestrzeniach unitarnych
Niech  będzie przestrzenią z iloczynem skalarnym i niech norma w
będzie przestrzenią z iloczynem skalarnym i niech norma w  będzie generowana tym iloczynem:
będzie generowana tym iloczynem:
 będzie przestrzenią z iloczynem skalarnym i niech norma w
będzie przestrzenią z iloczynem skalarnym i niech norma w  będzie generowana tym iloczynem:
będzie generowana tym iloczynem: .
.
Wtedy element najlepszej aproksymacji jest jedyny i jest określony następującą tożsamością
Aproksymacja funkcji
Aproksymacje można wykorzystać w sytuacji, gdy nie istnieje funkcja analityczna pozwalająca na wyznaczenie wartości dla dowolnego z jej argumentów, a jednocześnie wartości tej nieznanej funkcji są dla pewnego zbioru jej argumentów znane. Mogą to być na przykład wyniki badań aktywności biologicznej dla wielu konfiguracji leków. Do wyznaczenia aproksymowanej aktywności biologicznej nieznanego leku można wówczas zastosować jedną z wielu metod aproksymacyjnych.
Aproksymowanie funkcji może polegać na przybliżaniu jej za pomocą kombinacji liniowej tzw. funkcji bazowych.
Od funkcji aproksymującej, przybliżającej zadaną funkcję nie wymaga
się, aby przechodziła ona przez jakieś konkretne punkty, tak jak to ma
miejsce w interpolacji. Z matematycznego punktu widzenia aproksymacja funkcji  w pewnej przestrzeni Hilberta
w pewnej przestrzeni Hilberta  jest zagadnieniem polegającym na odnalezieniu pewnej funkcji
jest zagadnieniem polegającym na odnalezieniu pewnej funkcji  gdzie
gdzie  jest podprzestrzenią
jest podprzestrzenią  tj.
tj.  takiej, by odległość (w sensie obowiązującej w
takiej, by odległość (w sensie obowiązującej w  normy) między
normy) między  a
a  była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).
była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).
 w pewnej przestrzeni Hilberta
w pewnej przestrzeni Hilberta  jest zagadnieniem polegającym na odnalezieniu pewnej funkcji
jest zagadnieniem polegającym na odnalezieniu pewnej funkcji  gdzie
gdzie  jest podprzestrzenią
jest podprzestrzenią  tj.
tj.  takiej, by odległość (w sensie obowiązującej w
takiej, by odległość (w sensie obowiązującej w  normy) między
normy) między  a
a  była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).
była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).
Aproksymacja funkcji powoduje pojawienie się błędów, zwanych błędami
aproksymacji. Dużą zaletą aproksymacji w stosunku do interpolacji jest
to, że aby dobrze przybliżać, funkcja aproksymująca nie musi być wielomianem bardzo dużego stopnia (w ogóle nie musi być wielomianem).
Przybliżenie w tym wypadku rozumiane jest jako minimalizacja pewnej
funkcji błędu. Prawdopodobnie najpopularniejszą miarą tego błędu jest
średni błąd kwadratowy, ale możliwe są również inne funkcje błędu, jak
choćby błąd średni.
Istnieje wiele metod aproksymacyjnych. Jednymi z najbardziej popularnych są: aproksymacja średniokwadratowa i aproksymacja jednostajna oraz aproksymacja liniowa, gdzie funkcją bazową jest funkcja liniowa.
Wiele z metod aproksymacyjnych posiada fazę wstępną, zwaną również
fazą uczenia oraz fazę pracy. W fazie wstępnej, metody te wykorzystując
zadane pary punktów i odpowiadających im wartości aproksymacyjnych
niejako „dostosowują” swoją strukturę wewnętrzną zapisując dane, które
zostaną wykorzystane później w fazie pracy, gdzie dla zadanego punktu
dana metoda wygeneruje odpowiadającą mu wartość bądź wartości
aproksymowane. Funkcja aproksymująca może być przedstawiona w różnej
postaci. Najczęściej jest to postać:
- wielomianu (tzw. aproksymacja wielomianowa),
- funkcji sklejanych,
- funkcji matematycznych uzyskanych na drodze statystyki matematycznej (przede wszystkim regresji),
- sztucznych sieci neuronowych.
Funkcje aproksymujące w postaci wielomianu i funkcji sklejanych można
wykorzystać jedynie wtedy, gdy funkcja aproksymowana jest w postaci
jednej zmiennej.
Procesy losowe
Procesy losowe
- Definicja 1
- Procesem losowym nazywamy rodzinę zmiennych losowych

zależnych od parametru t i określonych na danej przestrzeni probabilistycznej (Ω,A,P).
Innymi słowy proces losowy to losowa funkcja parametru t, czyli taka funkcja, która  jest zmienną losowa.
jest zmienną losowa.
 jest zmienną losowa.
jest zmienną losowa.
Zmienną losową Xt, którą proces losowy jest w ustalonej chwili  nazywamy wartością tego procesu.
nazywamy wartością tego procesu.
 nazywamy wartością tego procesu.
nazywamy wartością tego procesu.
Zbiór wartości wszystkich zmiennych losowych  , nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
, nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
 , nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
, nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
Jeśli zbiór jest skończony lub przeliczalny, to mówimy o procesach
losowych z czasem dyskretnym. W pierwszym wypadku mamy do czynienia z
n-wymiarową zmienną losową, a w drugim z odpowiednim ciągiem zmiennych
losowych.
Choć niektóre klasy procesów losowych z czasem dyskretnym (np. łańcuchy
Markowa) zasługują na uwagę, to jednak w dalszym ciagu skoncentrujemy
się na procesach losowych z czasem ciągłym czyli takich, dla których T jest nieprzeliczalne.
Dla głębszego zrozumienia natury procesu losowego spójrzmy nań jeszcze z
innej strony. Jak pamiętamy zmienna losowa przyporządkowywała zdarzeniu
losowemu punkt w przestrzeni Rn.
W przypadku procesu losowego mamy do czynienia z sytuacją gdy do opisu
wyniku doświadczenia niezbędna jest funkcja ciągła, zwana realizacją
procesu losowego.
W dalszym ciągu zakładamy, że mamy do czynienia ze skończonymi funkcjami losowymi, a zbiór wszystkich takich funkcji (realizacji) będziemy nazywali przestrzenią realizacji procesu losowego. Prowadzi to do drugiej definicji:
W dalszym ciągu zakładamy, że mamy do czynienia ze skończonymi funkcjami losowymi, a zbiór wszystkich takich funkcji (realizacji) będziemy nazywali przestrzenią realizacji procesu losowego. Prowadzi to do drugiej definicji:
- Definicja 2
- Procesem losowym nazywamy mierzalną względem P transformację przestrzeni zdarzeń elementarnych Ω w przestrzeni realizacji, przy czym realizacją procesu losowego nazywamy każdą skończoną funkcją rzeczywistą zmiennej
 .
.
Definicja powyższa wynika ze spojrzenia na proces losowy jako na funkcję dwóch zmiennych  i
i  , ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
, ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
 i
i  , ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
, ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
Na ogół na przestrzeń realizacji procesu losowego narzuca się pewne
ograniczenia np. żeby to była przestrzeń Banacha (niezerowa i
zwyczajna).
Reasumując: graficznie można przedstawić te dwa punkty widzenia w następujacy sposób.
Pełne oznaczenie procesu losowego ma zatem postać
 , lub
, lub 
przy czym w obu wypadkach zakłada się, że jest określona przestrzeń probabilistyczna .
.
 , lub
, lub 
przy czym w obu wypadkach zakłada się, że jest określona przestrzeń probabilistyczna
 .
.
Ponieważ jednak zależność od ω jako naturalną zwykle się pomija, otrzymujemy:
 , lub
, lub  .
.
 , lub
, lub  .
.
Ponadto, jeśli zbiór T jest zdefiniowany na początku rozważań to pomija się także zapis  i w rezultacie otrzymujemy :
i w rezultacie otrzymujemy :
Xt, lub X(t).
 i w rezultacie otrzymujemy :
i w rezultacie otrzymujemy :Xt, lub X(t).
Oznaczenie X(t) może zatem dotyczyć całego procesu losowego, jego jednej realizacji (dla ustalonego ω) lub jego jednej wartości, czyli zmiennej losowej (dla ustalonego t). Z kontekstu jednoznacznie wynika, o co w danym zapisie chodzi.
Przejdźmy do zapisu procesu losowego X(t). Będziemy rozpatrywać wyłącznie procesy losowe rzeczywiste (proces losowy zespolony ma postać: X(t) = X1(t) + iX2(t), gdzie X1(t) i X2(t) są procesami losowymi rzeczywistymi).
Ponieważ  proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :
proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :
F(x,t) = P[X(t) < x]
 proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :
proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :F(x,t) = P[X(t) < x]
Oczywiście rozkład jednowymiarowy procesu losowego nie charakteryzuje
wzajemnej zależności między wartościami procesu (zmiennymi losowymi) w
różnych chwilach. Jest on zatem ogólny tylko wtedy gdy dla dowolnych
układow  wartości
procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół
nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład
wartości procesu w różnych chwilach.
wartości
procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół
nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład
wartości procesu w różnych chwilach.
 wartości
procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół
nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład
wartości procesu w różnych chwilach.
wartości
procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół
nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład
wartości procesu w różnych chwilach.- Definicja
- n-wymiarowym
rozkładem prawdopodobieństwa procesu losowego nazywamy łączny rozkład
prawdopodobieństwa i jego wartości dla dowolnego układu chwili t1,t2,...,tn , czyli łączny rozkład prawdopodobieństwa wektora losowego [X(t1),X(t2),...,X(tn)] opisany n - wymiarową dystrybuantą procesu losowego :
F(x1,t1;x2,t2;...;xn,tn) = P(X(t1) < x1,X(t2) < x2,...,X(tn) < xn) - Ruchy Browna − chaotyczne ruchy cząstek w płynie (cieczy lub gazie), wywołane zderzeniami zawiesiny z cząsteczkami płynu.
W 1827 roku szkocki biolog Robert Brown obserwując przez mikroskop pyłki kwiatowe w zawiesinie wodnej dostrzegł, iż znajdują się one w nieustannym, chaotycznym ruchu.
Ruchy Browna obserwuje się dla mikroskopijnych, mniejszych niż mikrometr, cząstek zawiesiny bez względu na ich rodzaj. Cząsteczki poruszają się ciągle, a ich ruch nie słabnie. Prędkość ruchu jest większa dla mniejszych cząstek i wyższej temperatury.
niedziela, 18 listopada 2012
Interpolacja
Interpolacja
Interpolacja
jest to metoda numeryczna polegająca na wyznaczaniu w danym przedziale tzw. funkcji interpolacyjnej. Przyjmuje ona w tym przedziale z góry zadane wartości w ustalonych punktach, nazywanych węzłami. Interpolacja stosowana jest często w naukach doświadczalnych, gdzie dysponuje się zazwyczaj skończoną liczbą danych do określenia zależności między wielkościami oraz w celu uproszczenia skomplikowanych funkcji, np. podczas całkowania numerycznego. Interpolacja jest szczególnym przypadkiem metod numerycznych typu aproksymacja.
Celem interpolacji jest znalezienie funkcji odpowiedniej klasy przechodzącej przez dany zestaw punktów (węzłów) w przestrzeni dwu- lub więcej wymiarowej.
Interpolacja ma zastosowanie w:
• szacowaniu określonych wielkości w punktach pośrednich,
• prowadzeniu gładkich krzywych lub powierzchni przez punkty pomiarowe lub z symulacji (funkcje sklejane),
• algorytmach numerycznych, np. znajdowaniu miejsc zerowych funkcji, różniczkowaniu i całkowaniu numerycznym.
Rodzaje interpolacji:
• liniowa
• trygonometryczna
• wielomianowa.
Interpolacja
jest to metoda numeryczna polegająca na wyznaczaniu w danym przedziale tzw. funkcji interpolacyjnej. Przyjmuje ona w tym przedziale z góry zadane wartości w ustalonych punktach, nazywanych węzłami. Interpolacja stosowana jest często w naukach doświadczalnych, gdzie dysponuje się zazwyczaj skończoną liczbą danych do określenia zależności między wielkościami oraz w celu uproszczenia skomplikowanych funkcji, np. podczas całkowania numerycznego. Interpolacja jest szczególnym przypadkiem metod numerycznych typu aproksymacja.
Celem interpolacji jest znalezienie funkcji odpowiedniej klasy przechodzącej przez dany zestaw punktów (węzłów) w przestrzeni dwu- lub więcej wymiarowej.
Interpolacja ma zastosowanie w:
• szacowaniu określonych wielkości w punktach pośrednich,
• prowadzeniu gładkich krzywych lub powierzchni przez punkty pomiarowe lub z symulacji (funkcje sklejane),
• algorytmach numerycznych, np. znajdowaniu miejsc zerowych funkcji, różniczkowaniu i całkowaniu numerycznym.
Rodzaje interpolacji:
• liniowa
• trygonometryczna
• wielomianowa.
Zmienne losowe
Zmienne losowe
Zmienna losowa – funkcja przypisująca zdarzeniom elementarnym liczby. Intuicyjnie: odwzorowanie przenoszące badania prawdopodobieństwa z niewygodnej przestrzeni probabilistycznej do dobrze znanej przestrzeni euklidesowej. Zmienne losowe to funkcje mierzalne względem przestrzeni probabilistycznych.
Zmienną losową jest na przykład funkcja opisującą wagę lub wzrost ciała wylosowanego z pewnej populacji osobnika. Zjawiskom o charakterze losowym, którym nie można w oczywisty sposób przypisać jakiejś miary liczbowej, można przypisywać liczby według pewnego klucza tak, aby możliwe było ich porównywanie w interesującym nas aspekcie. Najprostszymi przykładami są: moneta (np. orłu przypisujemy zero, a reszce jedynkę) i kostka do gry (każdej ściance przypisujemy liczbę wylosowanych oczek). Innymi przykładami mogą być: stan techniczny urządzenia, czy wiedza ucznia (oceniana w skali od 1 do 6).
Zmienną losową (rzeczywistą) na przestrzeni probabilistycznej nazywamy dowolną rzeczywistą funkcję mierzalną
nazywamy dowolną rzeczywistą funkcję mierzalną  , tzn. funkcję
, tzn. funkcję  spełniającą warunek
spełniającą warunek
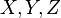 lub liter greckich
lub liter greckich  odmiennie niż zwykle zapisuje się funkcje.
odmiennie niż zwykle zapisuje się funkcje.
Przykłady:
Zmienna losowa – funkcja przypisująca zdarzeniom elementarnym liczby. Intuicyjnie: odwzorowanie przenoszące badania prawdopodobieństwa z niewygodnej przestrzeni probabilistycznej do dobrze znanej przestrzeni euklidesowej. Zmienne losowe to funkcje mierzalne względem przestrzeni probabilistycznych.
Zmienną losową jest na przykład funkcja opisującą wagę lub wzrost ciała wylosowanego z pewnej populacji osobnika. Zjawiskom o charakterze losowym, którym nie można w oczywisty sposób przypisać jakiejś miary liczbowej, można przypisywać liczby według pewnego klucza tak, aby możliwe było ich porównywanie w interesującym nas aspekcie. Najprostszymi przykładami są: moneta (np. orłu przypisujemy zero, a reszce jedynkę) i kostka do gry (każdej ściance przypisujemy liczbę wylosowanych oczek). Innymi przykładami mogą być: stan techniczny urządzenia, czy wiedza ucznia (oceniana w skali od 1 do 6).
Zmienną losową (rzeczywistą) na przestrzeni probabilistycznej
 nazywamy dowolną rzeczywistą funkcję mierzalną
nazywamy dowolną rzeczywistą funkcję mierzalną  , tzn. funkcję
, tzn. funkcję  spełniającą warunek
spełniającą warunek dla każdego zbioru borelowskiego
dla każdego zbioru borelowskiego  .
.
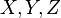 lub liter greckich
lub liter greckich  odmiennie niż zwykle zapisuje się funkcje.
odmiennie niż zwykle zapisuje się funkcje.Przykłady:
- Niech
 będzie zbiorem wszystkich możliwych wyników rzutu dwoma kośćmi do gry,
składa się on z 36 możliwych wyników. Przypisanie każdej kostce liczby
wyrzuconych oczek i zobrazowanie wyniku w postaci pary
będzie zbiorem wszystkich możliwych wyników rzutu dwoma kośćmi do gry,
składa się on z 36 możliwych wyników. Przypisanie każdej kostce liczby
wyrzuconych oczek i zobrazowanie wyniku w postaci pary  , gdzie
, gdzie  jest zmienną losową.
jest zmienną losową.
- Zmiennymi losowymi są również następujące funkcje: „iloczyn liczby oczek wyrzuconych na obu kostkach”, „suma liczby oczek wyrzuconych na obu kostkach”, „liczba oczek wyrzuconych na pierwszej z kostek”.
- Niech dane będą:
![\Omega = [0, 1],](http://upload.wikimedia.org/math/5/5/e/55ebdbdbad537c46664d69083283816c.png) σ-ciało
σ-ciało  zbiorów borelowskich przedziału
zbiorów borelowskich przedziału ![[0, 1]](http://upload.wikimedia.org/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) oraz określona na nim miara Lebesgue'a
oraz określona na nim miara Lebesgue'a  . Każda funkcja ciągła
. Każda funkcja ciągła  jest zmienną losową.
jest zmienną losową.
Subskrybuj:
Komentarze (Atom)




