niedziela, 18 listopada 2012

Zmienne losowe

Zmienne losowe

Zmienna losowa – funkcja przypisująca zdarzeniom elementarnym liczby. Intuicyjnie: odwzorowanie przenoszące badania prawdopodobieństwa z niewygodnej przestrzeni probabilistycznej do dobrze znanej przestrzeni euklidesowej. Zmienne losowe to funkcje mierzalne względem przestrzeni probabilistycznych.
Zmienną losową jest na przykład funkcja opisującą wagę lub wzrost ciała wylosowanego z pewnej populacji osobnika. Zjawiskom o charakterze losowym, którym nie można w oczywisty sposób przypisać jakiejś miary liczbowej, można przypisywać liczby według pewnego klucza tak, aby możliwe było ich porównywanie w interesującym nas aspekcie. Najprostszymi przykładami są: moneta (np. orłu przypisujemy zero, a reszce jedynkę) i kostka do gry (każdej ściance przypisujemy liczbę wylosowanych oczek). Innymi przykładami mogą być: stan techniczny urządzenia, czy wiedza ucznia (oceniana w skali od 1 do 6).

Zmienną losową (rzeczywistą) na przestrzeni probabilistycznej (\Omega, \mathcal F, P) nazywamy dowolną rzeczywistą funkcję mierzalną \xi \colon \Omega \to \mathbb{R}, tzn. funkcję \xi spełniającą warunek

\xi^{-1}(B)\in \mathcal{F} dla każdego zbioru borelowskiego B\subseteq \mathbb{R}.
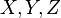Tradycyjnie zmienne losowe zapisuje się za pomocą wielkich liter z końca alfabetu, np. X, Y, Z lub liter greckich \xi, \eta, odmiennie niż zwykle zapisuje się funkcje.

 Przykłady:
  • Niech \Omega będzie zbiorem wszystkich możliwych wyników rzutu dwoma kośćmi do gry, składa się on z 36 możliwych wyników. Przypisanie każdej kostce liczby wyrzuconych oczek i zobrazowanie wyniku w postaci pary (i, j) \in R^2, gdzie 1 \leqslant i, j \le 6 jest zmienną losową.
Zmiennymi losowymi są również następujące funkcje: „iloczyn liczby oczek wyrzuconych na obu kostkach”, „suma liczby oczek wyrzuconych na obu kostkach”, „liczba oczek wyrzuconych na pierwszej z kostek”.
  • Niech dane będą: \Omega = [0, 1], σ-ciało \mathcal F zbiorów borelowskich przedziału [0, 1] oraz określona na nim miara Lebesgue'a P . Każda funkcja ciągła \xi : \Omega \to \mathbb R jest zmienną losową.
Autor: o

Brak komentarzy:

Prześlij komentarz

Subskrybuj: Komentarze do posta (Atom)